When a low viscosity fluid (for example, water) is injected
into a more viscous one, such as glycerin, an instability
occurs. The figure below shows an example of this instability
(often called Saffman-Taylor instability) in the Hele-Shaw
geometry, where blue water is injected into a colorless
glycerin. One important reason for studying this problem
is that it is closely related to many technologically
relevant ones, such as flow in porous media.

Main purpose of this project was to understand the
characteristics of the emerging patterns. A
variety of techniques were used to achieve this
goal:
a number of experiments were performed, where fluids,
injection rates, and separation between the plates were
varied. As an example, the movie below shows the
influence of the injection rate on the pattern formation
Movie: Water in Glycerin
students derived a governing equation (Darcy's law) that
models the dynamics in Hele-Shaw flow. Then, they performed
linear stability analysis, and compared their results to
the experimental ones;
numerical simulations of the governing equation were
performed. The results of this simulations were then
compared to both experiments, and the linear stability
analysis;
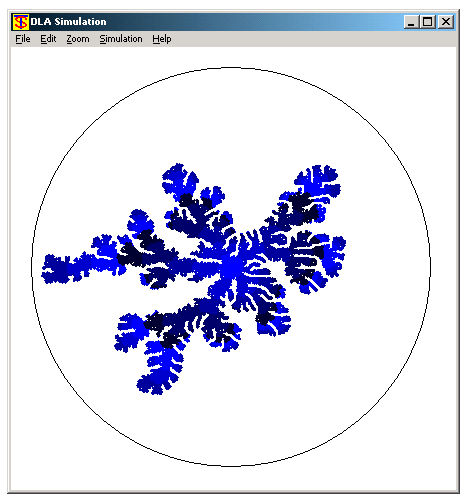
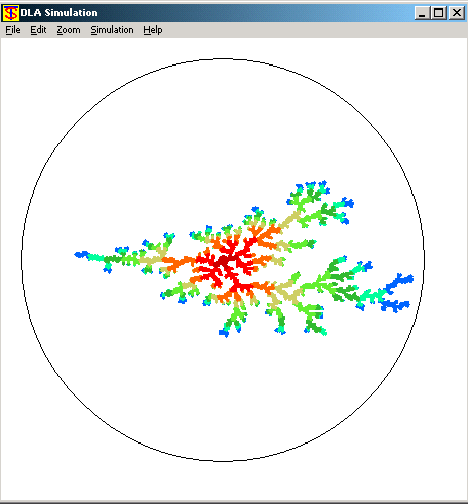
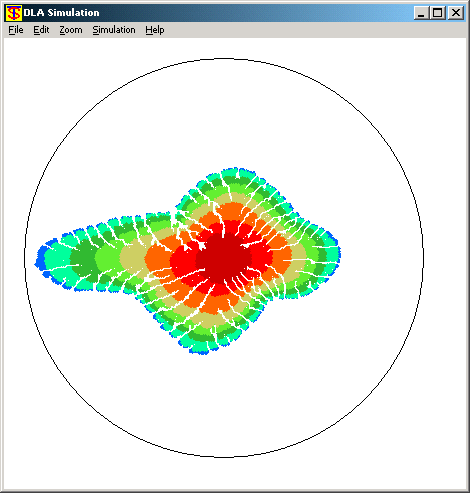
in a different, but related direction, discrete simulations
based on random walkers (diffusion limited aggregation) were
formulated. These simulations produced elaborate patterns,
shown in the figures below. The main difference between the
different results is the `sticking' rules determining how
random walkers stick to the interface. In this manner, the
resulting patterns model the experimental ones resulting
in the experiments where surface tension between the fluids
is varied. These simulations were presented by their author,
Tsezar Seman, at the 13th Annual Saint Joseph's University
Sigma Xi Student Research Symposium in Philadelphia, April 2002.